Aqueous interfaces: Bridging the gap between continuum and molecular models
The particulars of the electrostatic and hydrodynamic interactions at
the interface between charged objects and water are of immense
importance for biological systems, as well as for a wide range of
technological applications, such as gel electrophoresis and
electrokinetic pumping.
Despite the progress made in over a century of active research, the
intricate structure of aqueous interfaces remain poorly understood.
Using a two-scale modelling approach, we study the wide- ranging effects
of the ordered and anisotropic molecular structure of interfacial
water.
We extract molecular profiles of the dielectric function, the viscosity and the ionic free energy from atomistic molecular dynamics simulations, and incorporate this molecular information into continuum theory. The use of continuum theory enables us to reach length and time scales that are unattainable using only molecular dynamics simulations. At the same time, it provides us with the flexibility to easily vary system parameters such as geometry, salt concentration and surface charge density. One of the most significant advantages of this combination of molecular detail, flexibility of model parameters and sufficiently large scale is that it allows for direct comparison with experimental data.
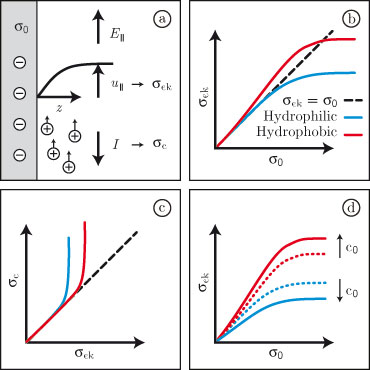
Incorporating the dielectric function and the viscosity profile into the combined Stokes and Poisson-Boltzmann equations accurately captures the saturation of the electro-osmotic flow velocity as a function of the bare surface charge density, which is consistently found in experiments on hydrophobic and hydrophilic surfaces (Fig. 1b).

Our multiscale modeling approach thus provides us with the means for experimental verification of our theoretical models, and simultaneously offers new insight into the molecular origin of experimental observations.
We extract molecular profiles of the dielectric function, the viscosity and the ionic free energy from atomistic molecular dynamics simulations, and incorporate this molecular information into continuum theory. The use of continuum theory enables us to reach length and time scales that are unattainable using only molecular dynamics simulations. At the same time, it provides us with the flexibility to easily vary system parameters such as geometry, salt concentration and surface charge density. One of the most significant advantages of this combination of molecular detail, flexibility of model parameters and sufficiently large scale is that it allows for direct comparison with experimental data.
Incorporating the dielectric function and the viscosity profile into the combined Stokes and Poisson-Boltzmann equations accurately captures the saturation of the electro-osmotic flow velocity as a function of the bare surface charge density, which is consistently found in experiments on hydrophobic and hydrophilic surfaces (Fig. 1b).

Cover image source: American Chemical Society.

Fig. 1.
(a) An electric field parallel to a surface carrying a bare surface charge density σ0 produces an electro-osmotic flow profile, from which the electrokinetic surface charge density σek is calculated.
The conductive surface charge density σc is calculated from the electric current I.
(b) σek is experimentally found to saturate as a function of σ0; saturation occurs at higher values for hydrophobic surfaces than for hydrophilic surfaces.
(c) σc exceeds σek at all surface types.
(d) When the bulk salt concentration c0 is raised, σek increases at hydrophobic surfaces, and decreases at hydrophilic surfaces.
Moreover, the experimentally well-established
excess surface conductivity (Fig. 1c), generally
referred to as anomalous surface conductivity,
follows directly from the same model.
The latter result makes the assumption of electrical conductance through
otherwise static water layers — which has been the common explanation
of the experimental observations — superfluous.
Finally, the dependence of the electro-osmotic flow velocity on the bulk
salt concentration (Fig. 1d) is explained by the same combination of
dielectic and hydrodynamic surface effects [1,2].
Our multiscale modeling approach thus provides us with the means for experimental verification of our theoretical models, and simultaneously offers new insight into the molecular origin of experimental observations.
| [2] | D. J. Bonthuis and R. R. Netz; Unraveling the combined effects of dielectric and viscosity profiles on surface capacitance, electro-osmotic mobility, and electric surface conductivity; Langmuir 28, 16049 (2012) |
| [1] | D. J. Bonthuis and R. R. Netz; Beyond the continuum: How molecular solvent structure affects electrostatics and hydrodynamics at solid-electrolyte interfaces; J. Chem. Phys. B 117, 11397 (2013) |